Difference between revisions of "Hex theory"
(Added some proofs / proof sketches. Also added winning strategy for non-square boards.) |
(→Winning strategy for non-square boards: Also first-player winning.) |
||
| Line 27: | Line 27: | ||
An analogous strategy works for all boards of size ''n''×''m'' with ''n'' > ''m''. If the difference between ''n'' and ''m'' is greater than 1, Blue can simply ignore the additional rows, say at the bottom of the board, i.e., pretend that they have already been filled with Red pieces. If Red moves in the ignored area, Blue can play anywhere. If Blue's strategy later requires moving in a cell where Blue has already moved, Blue can again just move anywhere. | An analogous strategy works for all boards of size ''n''×''m'' with ''n'' > ''m''. If the difference between ''n'' and ''m'' is greater than 1, Blue can simply ignore the additional rows, say at the bottom of the board, i.e., pretend that they have already been filled with Red pieces. If Red moves in the ignored area, Blue can play anywhere. If Blue's strategy later requires moving in a cell where Blue has already moved, Blue can again just move anywhere. | ||
| + | |||
| + | Since we showed that Blue has a second-player winning strategy, it follows that Blue also has a first-player winning strategy, since the additional move cannot hurt Blue. | ||
For symmetric reasons, Red has a winning strategy when ''n'' < ''m''. | For symmetric reasons, Red has a winning strategy when ''n'' < ''m''. | ||
Revision as of 00:48, 14 June 2020
Unlike many other games, it is possible to say certain things about Hex, with absolute certainty. Whether this makes Hex a better game is of course debatable, but many find this attribute charming.
The most important properties of Hex are the following:
Contents
Winning Strategy
- When the swap option is not used, the first player has a winning strategy.
- When playing with the swap option, the second player has a winning strategy.
- On non-square boards, i.e., boards of size n×m, where n≠m, the player with the shorter distance to cover has a winning strategy regardless of who starts.
These first and third statements are proved below. The second statement is a simply consequence of the swap rule: since Hex has now draws, each move is either winning or losing. If the opening move would be winning without the swap rule, the second player swaps and inherits the win. If the opening move would be losing, the second player declines to swap and goes on to win. Thus, the second player can always win.
No winning strategy for Blue
In chess, while nobody seriously believes that black has a winning strategy, nobody has been able to disprove it. On the other hand, in Hex, a simple strategy-stealing argument shows that the second player cannot have a winning strategy, and therefore the first player must have one.
In fact, we can prove a more general statement: for boards of size n×'n, any position that is symmetric (i.e., invariant by reflection about the short or long diagonal and inverting the color of the pieces) is a winning position for the next player to move under optimal play. This follows from the fact that Hex is a monotone game: a position with additional pieces of a player's color is always at least as good for that player as the position without the additional pieces. If "passing" were allowed, it would therefore never be to a player's advantage to pass. If the second player to move had a winning strategy for a symmetric position, then the first player to move could simply steal that strategy by passing and therefore themselves becoming the second player to move. Since passing does not help the player, they also have a winning strategy without passing, contradicting the assumption that the other player was winning.
Winning strategy for non-square boards
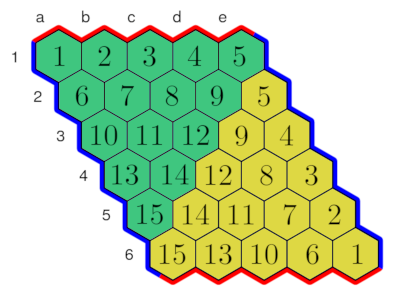
Consider a board of size (n+1) × n. In this case, Blue has a shorter distance to cover than Red. Blue has the following second-player winning strategy. Divide the board into two triangles as shown.
Now whenever Red plays in the yellow triangle, Blue responds by playing in the cell of the same number in the green triangle, and vice versa. After filling all of the cells in the way, Red cannot have a winning path, for consider the bottom-most green cell that is adjacent to the yellow triangle and that is connected to Red's top edge. Then by symmetry, Blue has a connection from the same-numbered cell in the yellow triangle to Blue's right edge, blocking any possible connection by Red to the bottom edge.
An analogous strategy works for all boards of size n×m with n > m. If the difference between n and m is greater than 1, Blue can simply ignore the additional rows, say at the bottom of the board, i.e., pretend that they have already been filled with Red pieces. If Red moves in the ignored area, Blue can play anywhere. If Blue's strategy later requires moving in a cell where Blue has already moved, Blue can again just move anywhere.
Since we showed that Blue has a second-player winning strategy, it follows that Blue also has a first-player winning strategy, since the additional move cannot hurt Blue.
For symmetric reasons, Red has a winning strategy when n < m.
No draw
If a Hex board is full then there is one and only one player connecting their edges. See also draw. The proof idea is quite simple. On a full Hex board, consider the set A of all red cells that are connected to Red's top edge. If this set contains a cell on Red's bottom edge, then Red is the winner. Otherwise, Blue has a winning path by going along the boundary of A.
== Complexity ==
- The decision problem associated to generalised Hex is PSPACE-complete.
- The detection of dominated cells is NP-complete. (To be checked then sourced)
- The detection of the virtual connections is PSPACE-complete. Reference here
Solving Hex
- Hex has been solved on small boards.
- The game can not end in a draw. (Proofs on Javhar's page)
See also
External links
- Thomas Maarup masters thesis