Difference between revisions of "Handicap"

Revision as of 15:10, 8 October 2006

Playing with handicap means to give one of the players (preferably the weaker one) an advantage at the start of the game. The point of this is to make the game more even, so that it will be challenging for both players.

In Hex there is no standard way of playing with handicap, and because of this it is not very common to do so. This ought to be changed.

There are several ways a handicap could be implemented.

Non-rhombic board

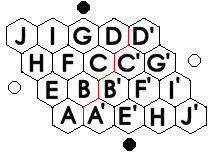
One natural way is to play with an m × n board where m is distinct from n, and let the weaker player have the shortest distance between his sides. Unfortunately, this doesn't work very well, since there exists an easy, explicit winning strategy for the player with shortest distance.

Here is the winning strategy. Suppose the board is an m by m+1 grid. The diagram shows m=4. The board can be partitioned into two triangular regions of m cells on each side. Now pair each cell in one triangle with a cell in the other triangle, as shown. The pairing is like a mirror image which is shifted slightly. The winning strategy for black is to answer each white move by playing in the corresponding cell in the other triangular region. If black has already occupied the corresponding cell, then it does not matter where black plays.

Suppose the board is filled with stones, and white has a win despite the fact that black followed this strategy. That implies the winning white path must cross the red line at least once. Consider the highest point at which the winning white path crosses the red line. This crossing cannot occur between two white stones on the same horizontal row, since for each such pair of cells, black must have occupied one of them. That implies the crossing from left to right must "go down" from B to A' or C to B' etc. Let us call this pair of cells Y (on the left side of the red line) and X' on the right side. The corresponding cell to Y we will call Y'.

For white to have a winning path which crosses at this point, there must be a continuous chain of white stones from cell Y to the left white border row. But since black followed the above strategy, this implies there is a continuous chain of corresponding black stones from Y' down to the bottom black border row. Therefore the white chain is blocked from connecting to the right. This contradicts the assumption that white has a win, so black must have a win.

For other shape grids, m by m+k where k>1, the same strategy can be used, as long as the two triangular regions are adjacent to each other. For cells which lie outside these regions on the left or right, it does not matter how black responds to any white moves in these regions. --David 17:10, 8 Oct 2006 (CEST)

Start with pieces on the board

Alternatively one can use the kind of handicap used in Go: The weaker player places a certain number of pieces on the board as his first move. A 1-piece handicap is the same as playing ordinary Hex without the swap option. With a handicap of two or more pieces, the first player either places the stones as he likes, or according to some pre-defined rules.

The drawback of this option is that even a 1-piece handicap gives a very big advantage. At least this is true on smaller boards (such as the 10 × 10 board). On larger boards, such as 19 × 19 this may be a good solution, and weak players may even be allowed to place three or four pieces against the strongest players.